Moon and Magnetotail

Identifying and Visualizing the Moon’s Position with respect to the Earth’s Magnetotail

GitHub Repository: Moon-and-Magnetotail

DOI:

This work contributed in a small way to the experimental design of the Deep Space Radiation Genomics (DSRG) experiment on Artemis 1. The DSRG experiment will orbit the moon, and the goal of the experiment is to expose a collection of yeast to a space radiation environment similar to that expected for a trip beyond Earth’s protective magnetospheric environment. This will enable the analysis of the effect of microgravity and space radiation in genes.

To ensure the experiment encounters ‘pristine’ solar wind conditions, it is important to avoid data collection during the spacecraft’s (and consequently, the moon’s) transit through the magnetotail. The solar wind interacts with the Earth’s magnetic field to form the magnetosphere, which includes a long tail that acts as a barrier to energetic particles.

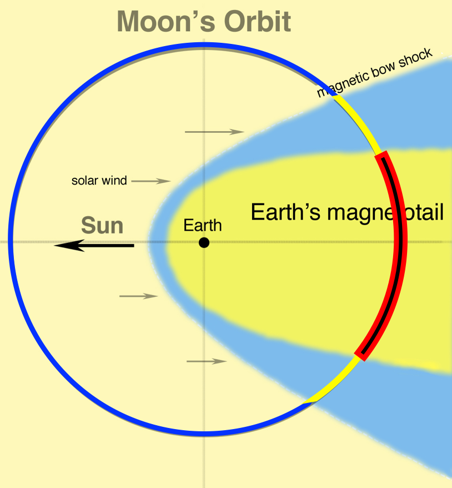
Modified from Tim Stubbs/University of Maryland/GSFC, accessed from nasa.gov

This is where our team - Valerie Bernstein (myself), Kaiya Wahl, and Delores Knipp - step in as space weather researchers! Our specific goal was to predict the position of the moon with respect to the magnetotail between given start and end dates in order to provide a yes/no decision table for data collection times.

It is important for the DSRG experiment to collect data for 3 days at a time and be conducted while in the free-flowing solar wind outside the magnetotail and bow shock. To accurately predict which times the experiment should or should not take place, the moon’s position is calculated and compared to the position of the magnetotail and bow shock.

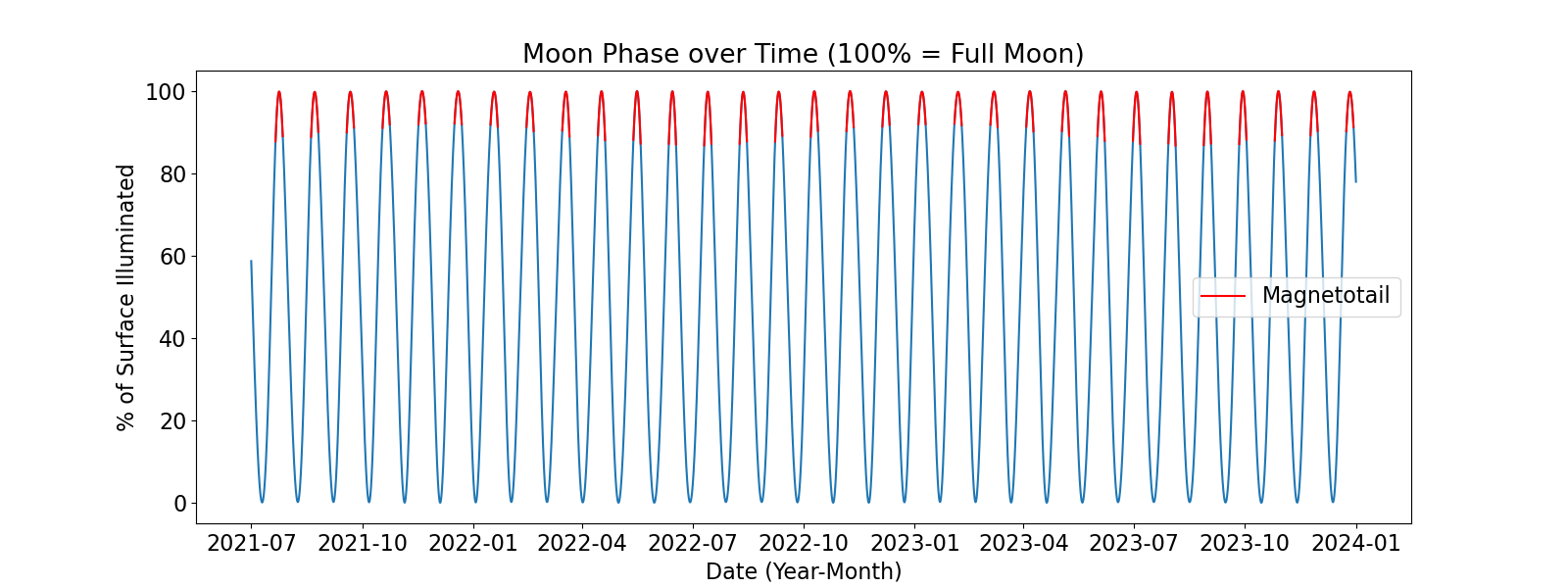
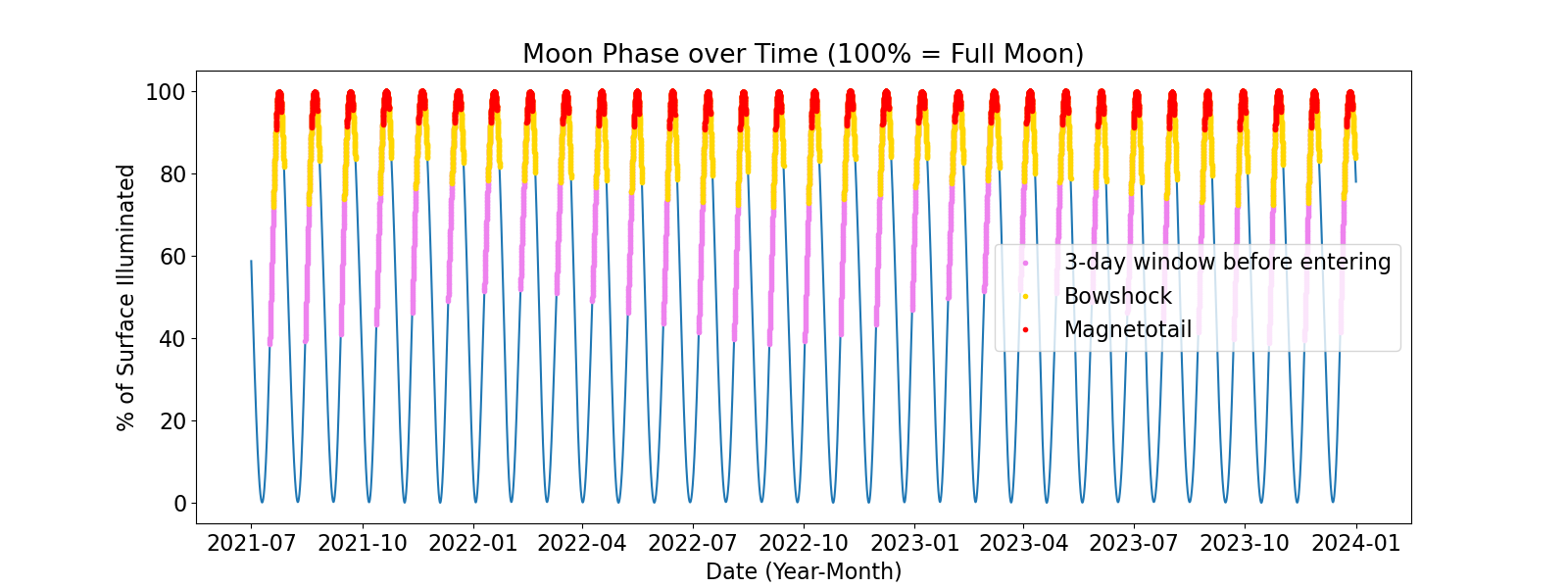
The Python astronomical ephemeris library PyEphem, developed by Rhodes (2011), is used to calculate the moon’s right ascension (RA), declination (dec), and distance from the Earth given a specified date and time. PyEphem is also used to compute the moon phase at a specified time, which is given as the percentage of the moon’s surface that is illuminated. We compute the moon’s RA, dec, and phase every hour between the specified start and end dates. We also identify full moon times, when the surface illumination = 100%. Below is a plot of the moon phase from 2021 to 2024, where the red highlighted areas indicate the approximate 6 day windows in which the moon passes inside the magnetotail.

To quantify the magnetotail transit times more precisely than using the 6-day window estimate, we covert the PyEphem-provided lunar position in RA and dec (which are Geocentric Equatorial Inertial, or GEI, coordinates) into Geocentric Solar Ecliptic (GSE) coordinates. This coordinate conversion is performed because the magnetotail lies in the Sun-Earth ecliptic plane. The coordinate conversion is provided by M. Hapgood (1992) and outlined below.

In the above equation, square brackets indicate matrices, x, y, and z indicate cartesian vector components, and T is the transformation matrix. T is defined as the matrix multiplication of two rotation matrices:

where is a rotation by the angle (the Sun’s ecliptic longitude) about the z-axis, and is a rotation by the angle (the obliquity of the ecliptic) about the x-axis. These two rotations represent the rotation from Earth’s equator to the ecliptic plane and the rotation in the ecliptic plane from the First Point of Aries to the Earth-Sun direction. The GSE coordinate are defined such that the +x direction is pointed from the Earth to the Sun, the +y direction is pointed towards dusk, and +z is in the northward direction out of the ecliptic plane. For further information about how to obtain the angle necessary to perform these rotations, please refer to M. Hapgood (1992).

Given the moon’s position in GSE coordinates, we find the intersection of the lunar orbit with the bounds of the magnetotail and bow shock in GSE coordinates. Since the moon’s orbital radius is ~60 in the ecliptic plane, the moon will intersect with the magnetotail at ~60 in the negative x direction. Therefore for this analysis, the magnetotail and bow shock are drawn as 2D circles in the y-z plane at . The magnetotail circle is centered (in GSE x,y, and z components) at , with a radius of 30. The position of the magnetotail is aberrated in the +y direction, and this aberration is defined as:

where is the absolute value of the x-component of the moon’s GSE position, and is the solar wind velocity in units of km/s. This offset reflects the aberration of the magnetotail due to Earth’s motion around the sun (average speed being 29 km/s) (Hapgood, 2007, and personal communication). We use a typical solar wind speed of 400 km/s. The bow shock circle is centered around the magnetotail with a radius of ~50 (Sibeck & Lin, 2014). The following plots show the moon’s orbit in GSE coordinates over the course of 3 years as well as the 2D cross-sections of the magnetotail and bow shock (the inner and outer black circles).

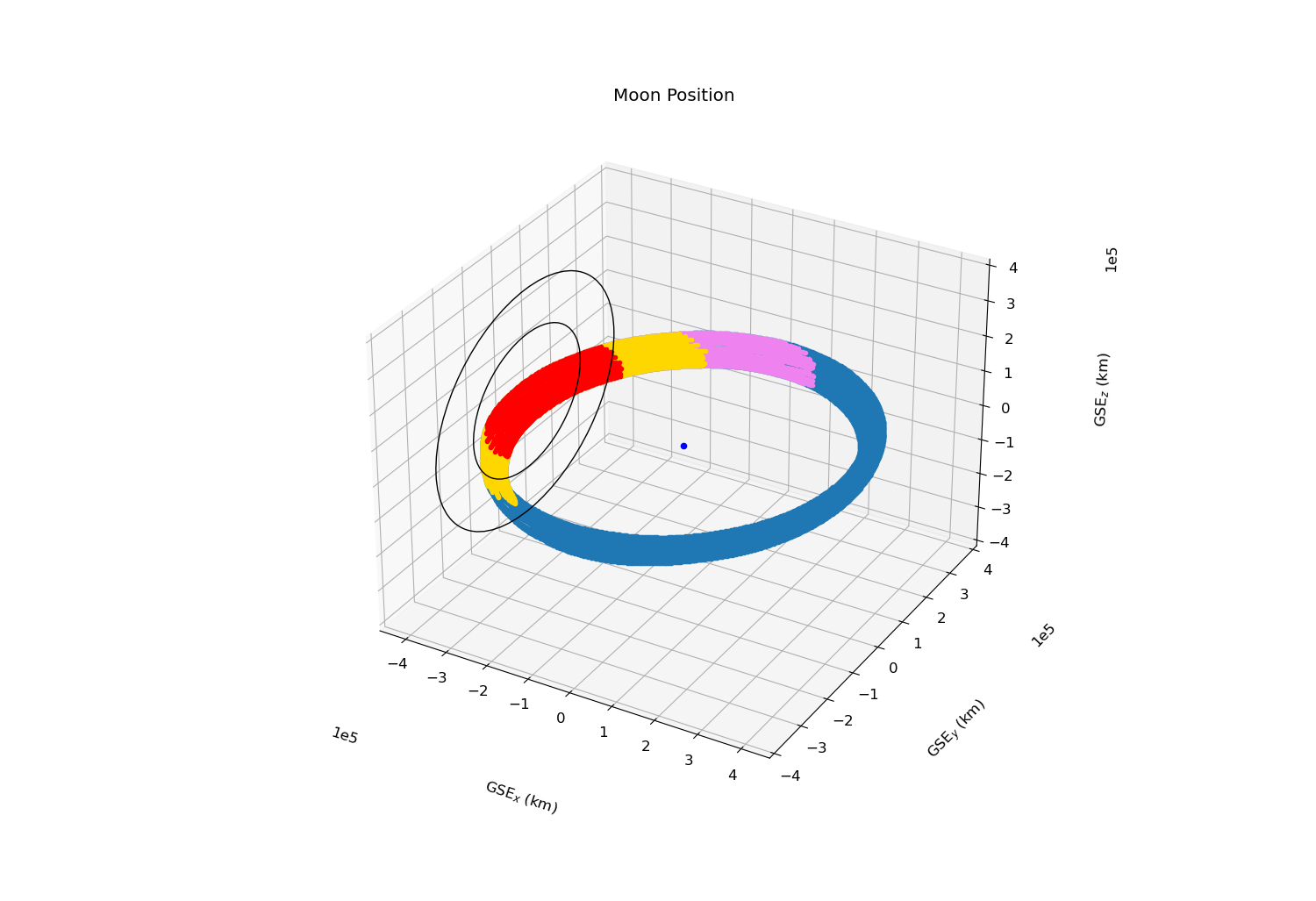
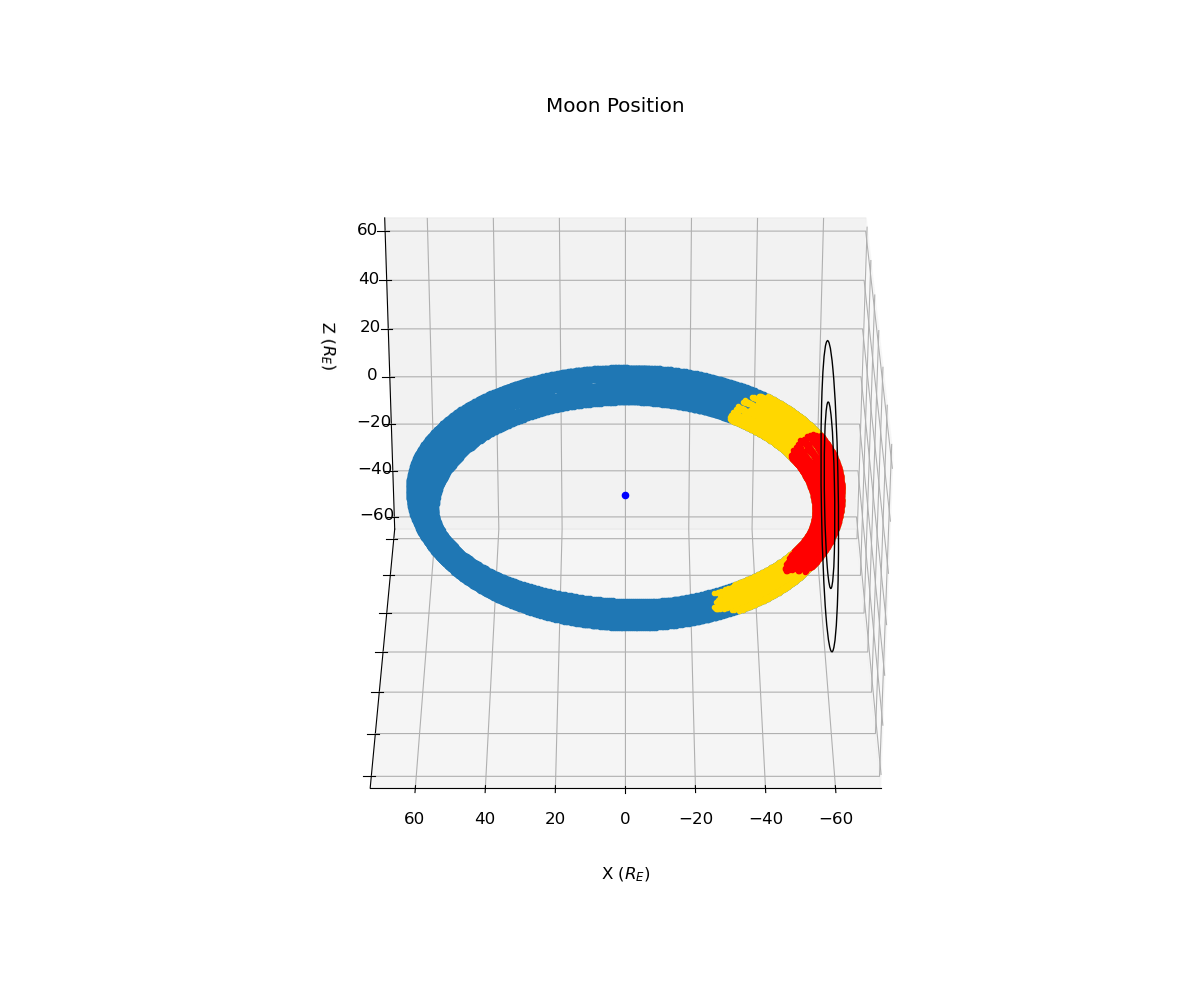
In the above images, the Earth is located at (0,0,0). The purple data points represent the three days to be excluded from the “Yes” DSRG data collection dates prior to the moon’s intersection with the bow shock. The yellow data points represent when the moon is transiting the bow shock, and the red data points represent when the moon is transiting the magnetotail. We also plot the moon phase over time, where the 3-day window prior to the moon entering the bow shock, the bow shock transit times, and the magnetotail transit times are all overlaid and distinguished by the same color scheme as the above plots.

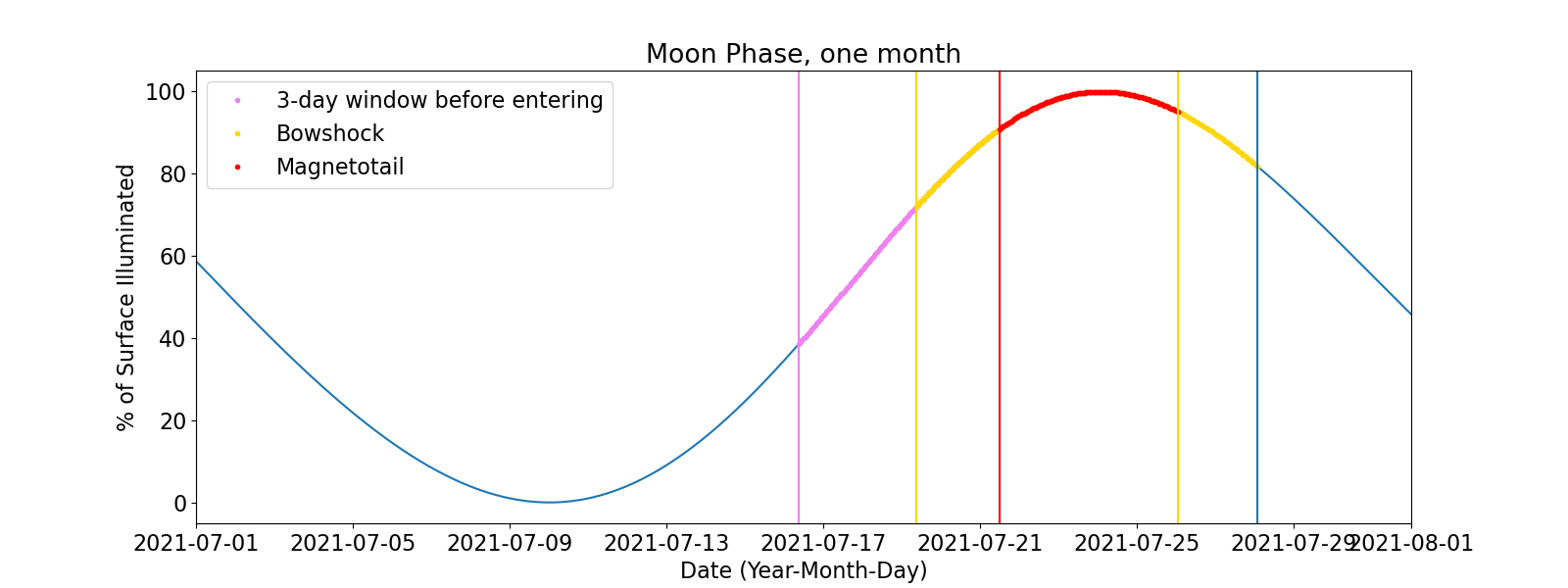
We can also display a zoomed-in view of this phase plot for a single lunar cycle (one month). This allows for a closer look at how much time the moon spends inside the bow shock and magnetotail in a month. Vertical lines indicate the times when the moon enters the regions of interest.

You can find all of the publications and presentations associated with this project under the References tab of this ResearchGate Project Page.